Цифры - страница 2
Египетская система была построена на основе строго выдержанного десятичного принципа.
Особые знаки имелись только для единицы и различных степеней от числа 10; для единицы применялся знак в форме горизонтальной, реже вертикальной черточки, для десяти — дуга, для сотни — загнутая веревка, для тысячи — стебель лотоса, для десяти тысяч — нечто вроде согнутого пальца, для сотни тысяч — головастик (потому что головастики выводятся в очень больших количествах), а для миллиона — знак в виде фигурки человека, поднявшего руки в изумлении перед таким огромным числом.
Все остальные числа получались по принципу сложения указанных основных цифр, поставленных рядом; так, для написания числа 375 повторяли три раза знак «сотни», семь раз — знак «десятки» и пять раз — знак «единицы».
Цифровые знаки начали применяться в Египте с глубокой древности, в додинастическую эпоху, когда египетское письмо еще только переходило от пиктографии к логографии; так, в надписи фараона Нармера (конец IV тысячелетия до н.э.) имеются знаки (стебли лотоса), которые читаются как обозначения тысяч. Начиная с периода «Среднего царства», обозначение крупных чисел строилось не по принципу сложения, а по принципу умножения; в этом случае крупное число делилось на два сомножителя, меньший из которых (например, единицы) писался под большим (например, под тысячами).
В иератическом и демотическом письме цифровые знаки приобрели скорописную форму; кроме того, появились особые знаки почти для всех единиц и десятков. В египетских дробях числителем обычно была единица; так, дробь 4/15 обозначали как сумму 1/5 и 1/15 (папирус Ахмеса, начало II тысячелетия до н.э.).
Близка к египетской критско-микенская система цифр, тоже построенная по десятичному принципу. Особые знаки имелись здесь для единицы (вначале точка, позже вертикальная черточка), десятки (горизонтальная черточка), сотни (круг), тысячи (круг с черточками); позже появился особый знак и для десяти тысяч.
При написании числа каждый из этих знаков повторялся столько раз, сколько было в числе единиц, десятков и сотен; так при написании числа 237 два раза повторялся знак «сотни» (круг), три раза — знак «десятки» (горизонтальная черта) и семь раз — знак «единицы» (вертикальная черта). Имелись особые обозначения для сложения, суммы и т.д.; применялась, согласно А. Эвансу, также система процентов.
Близка к египетской (в ее иератически-демотическом варианте) также китайская цифровая систем. Система эта тоже строилась на десятичном принципе; однако особые знаки имелись в ней не только для единицы и различных степеней от числа 10, но и для других чисел. Наряду с принципом сложения знаков применялся принцип умножения; так, число 400 иногда передавалось знаком 100 с надписанными над ним (или влево от него) знаком 4.
Наибольшим своеобразием, чрезвычайной сложностью и в то же время использованием новых, передовых принципов цифрового счисления отличались переднеазиатские цифровые системы.
Простейшие цифровые обозначения точечного типа встречаются в самых древних шумерских надписях середины IV тысячелетия до н.э. Позднее в связи с возросшими требованиями хозяйства и торговли цифровые системы Передней Азии переживают быстрое развитие.
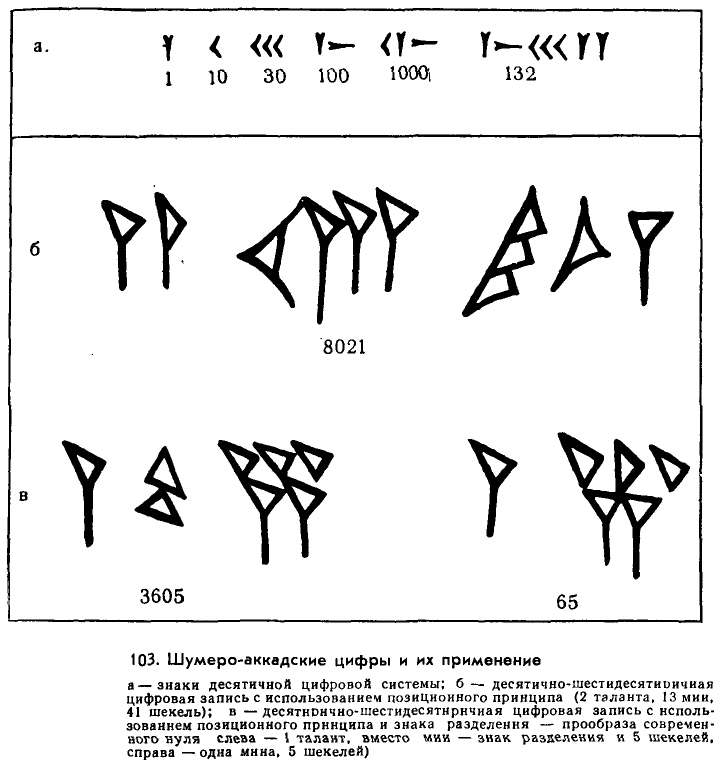
Одна из этих систем, более простая и построенная на последовательном десятичном принципе, была сходна с египетской. Система эта имела особые знаки для «единицы» (вертикальный клин), для «десятки» (вертикальный угол), для «сотни» (вертикальный и горизонтальный клинья) и для «тысячи» (соединение, как бы умножение знаков «десять» и «сто»). Все остальные числа получались по принципу сложения основных цифр: так, для обозначения числа 132 писали: один раз знак сотни, три раза знак десятки и два раза знак единицы.
Своеобразнее, но сложнее была другая цифровая система Передней Азии, сочетавшая десятичный принцип с шестидесятеричным. Появление у народов Передней Азии шестидесятеричного принципа счета многие исследователи объясняют тем, что этими народами издавна применялись две весовые единицы — шумерская «мина» и аккадский «шекель», причем «мина» была в 60 раз крупнее «шекеля»; позднее возникла также третья единица «талант», который равнялся 60 «минам».
Наличие таких трех единиц, из которых каждая большая равнялась 60 меньшим, привело к тому, что шумеро-аккадские система счета и система цифр оказались построены на сочетании десятичного и шестидесятеричного принципа. Так, вместо того, чтобы говорить «восемь тысяч двадцать один», говорили: «Два таланта (3600х2), тринадцать мин (60х13) и сорок один шекель (41)». Соответственно строилась и цифровая запись этого числа.
Такое построение обусловило появление позиционного принципа: значение цифры стало зависеть не только от ее формы, но и от места в сложной числовой записи. Так, первый из двух основных знаков этой системы — вертикальный клин — в зависимости от его места в сложном числе мог обозначать: единицу (один («шекель»), 60 (одну «мину») и 3600 (один «талант»); соответственно второй из основных знаков — вертикальный угол — мог обозначать: 10 (десять «шекелей»), 600 (десять «мин») и 36 000 (десять «талантов»).
Знаки, обозначавшие «таланты», всегда писали перед знаками «мин», а знаки «мин» перед «шекелями», с отделением каждого из этих разрядов цифр пробелами. Но такая запись чисел оказалась неудобной, когда в ней отсутствовал средний разряд («мины»); числа 65 (одна «мина», пять «шекелей») и 3605 (один «талант», пять «шекелей») писались одинаково. Поэтому позже был введен особый знак разделения (два косых клина, расположенные один на другом); знак этот указывал, что в цифровой записи отсутствуют единицы того разряда, на месте которого стоял этот знак. Знак этот явился прообразом современного нуля.
По особому строились дроби: их знаменатель равнялся 6, 60, 360, 3600, 36 000; так вместо 1/2 писали 3/6, вместо 2/3 писали 4/6 и т.п.
В целом переднеазиатская система цифр (также как и система клинописи) была очень сложной. В то же время она оказалась и наиболее прогрессивной из древнейших цифровых систем; в ней впервые были применены позиционный принцип и особый знак (прообраз нуля) для обозначения отсутствия данного разряда цифр. Как отмечает В.В. Струве, пережитки переднеазиатской шестидесятеричной системы сохранились до нашего времени; так, час делится на 60 минут, минута — на 60 секунд, окружность — на 360 градусов и т.д.
Особый характер имели цифровые системы майя и ацтеков. Системы эти были построены на пятеричном принципе счета, иногда осложняемом двадцатеричным. Особые знаки имелись для «единицы» (точка), «пяти» (черточка), «двадцати» (у ацтеков — знамя); кроме того, иногда использовались особые знаки для «четырехсот» (20х20), для «восьми тысяч» (400х20) и т.д. Остальные числа получались путем повторения (сложения) основных цифровых знаков.